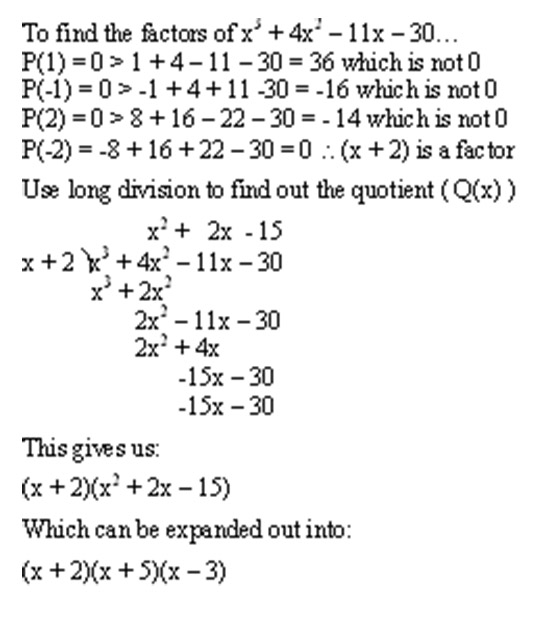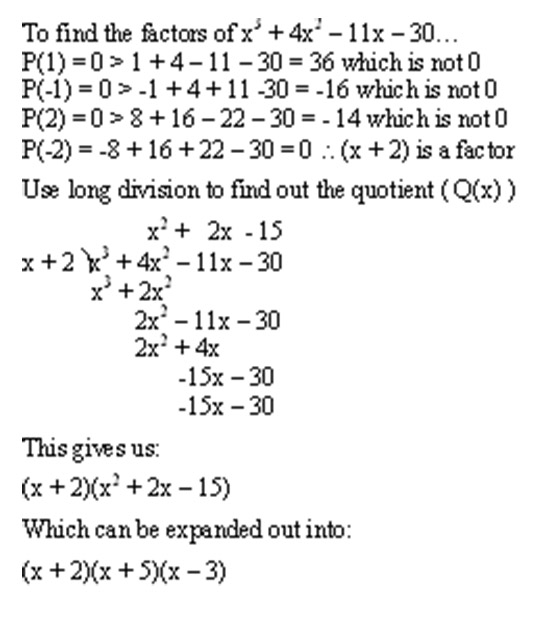
Factor theorem is a specialised use of Remainder Theorem, when for a certain polynomial expression ( P(x) ), written as
P(x) = (x-a)Q(x) + R
There is no remainder (ie, P(x) = (x-a)Q(x), or P(a) = 0)
When this is the case, solving for P(a)=0 (initially through trial and error, starting with a=1, then a=-1, a=2 and so on, until one pops up) will give a factor in the equation. Factor theorem can continue to be used for the rest of the equation - Q(x) - until it is broken down into individual factors.